ADS
Bases y alturas
bloque-iiDesafío 28Libro Desafíos Matemáticos Quinto grado Contestado
Ciclo Escolar: 2014|2015|2016|2017
Instrucciones
Objetivo de la lección:- Que los alumnos identifiquen las bases y alturas correspondientes en triángulos obtenidos al trazar una diagonal en cuadrados, rectángulos, trapecios y paralelogramos.
Consigna:
En parejas, calculen el área de los dos triángulos de cada figura, verifiquen si la suma de estas áreas equivale al área de la figura completa. Consideren como unidad de superficie un cuadrito y como unidad de longitud un lado de cuadrito.
Para contestar esta consigna hay que contar cuantos cuadritos abarca cada figura.
Primero contemos los cuadros de los triángulos de esta manera:

La consigna te dice además, que sumes las áreas de cada triángulo para saber si equivale al área de la figura completa. Así:

Como ves, los triángulos en esta figura tienen un área de 12.5 u2 cada uno y la suma de sus áreas si equivale al área de la figura completa, el cuadrado, porque: 12.5 + 12.5 = 25
Antes de continuar repasemos el objetivo de la lección: "Que los alumnos identifiquen las bases y alturas correspondientes en triángulos obtenidos al trazar una diagonal en cuadrados, rectángulos, trapecios y paralelogramos."
Por lo tanto notemos que la base del triangulo tiene de longitud 5 cuadritos y su altura en este ejemplo también 5. Multipliquemos 5x5 = 25 pero como son dos triángulos dividimos ese resultado entre dos, así: 25/2 = 12.5 obtenemos el área de cada triangulo.

Concluimos entonces que el área de un triangulo es igual a base x altura entre dos.
Veamos ahora la demás figuras:
Figura Romboide:
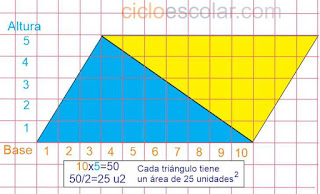
Figura Rectángulo:

En el caso del trapecio, los dos triángulos que lo forman son diferentes y, por lo tanto, no tienen la misma área; pero si sacamos el área de los dos triángulos es decir multiplicar la suma de las bases por la altura y dividir el resultado entre 2.


Que kulo
ResponderEliminar